В мире геометрии не всегда возможно представить фигуру в виде идеальных прямоугольников, треугольников или кругов. Она может быть кривой, извилистой и несимметричной. В таких случаях невозможно применить стандартные формулы для расчета площади. Однако существуют специальные методы и алгоритмы, которые позволяют определить площадь фигуры неправильной формы.
Один из таких методов – метод разделения фигуры на более простые геометрические фигуры. Он заключается в том, чтобы поделить сложную фигуру на несколько более простых, например, на треугольники или прямоугольники, для которых существуют простые формулы расчета площади. Затем найденные площади суммируются, чтобы получить общую площадь. При этом важно выбрать такое разбиение, которое максимально приближает исходную фигуру.
Другой метод – метод аппроксимации. Он используется, когда невозможно разделить фигуру на простые геометрические фигуры или когда фигура имеет очень сложную форму. Метод аппроксимации заключается в том, чтобы приближенно представить фигуру геометрической фигурой, для которой существует простая формула расчета площади. Это может быть, например, прямоугольник или круг, который лучше всего соответствуют исходной фигуре. Затем найденная площадь аппроксимирующей фигуры используется как приближенная площадь исходной фигуры.
Разбейте фигуру на более простые формы
Для определения площади фигуры неправильной формы мы можем использовать метод разбиения этой фигуры на более простые формы. Этот подход позволяет нам упростить задачу и применить знания о площади прямоугольников, треугольников и кругов для решения.
Когда мы разбиваем фигуру на более простые формы, мы можем выразить ее площадь суммой площадей этих простых форм. Для этого мы должны разделить фигуру на различные части, каждая из которых может быть представлена как прямоугольник, треугольник или круг. Затем мы можем вычислить площадь каждой части и сложить их вместе, чтобы получить общую площадь фигуры.
| Форма | Площадь |
|---|---|
| Прямоугольник | 15 кв.м |
| Треугольник | 8 кв.м |
| Круг | 12 кв.м |
Как видно из таблицы, мы разбили фигуру на прямоугольник, треугольник и круг. Затем мы вычислили площадь каждой формы и сложили их вместе, чтобы получить общую площадь фигуры, которая равна 35 квадратным метрам. Таким образом, разбиение фигуры на более простые формы помогло нам решить задачу и найти ее площадь.
Разбейте фигуру на более простые формы
При решении задач на определение площади неправильной фигуры методом разбиения ее на более простые формы, необходимо внимательно рассмотреть ее структуру и выделить основные элементы, которые можно представить в виде более простых геометрических фигур. Такой подход позволяет разбить сложную фигуру на более мелкие участки, для которых уже существуют известные формулы и алгоритмы расчета площади.
Использование треугольников
Один из методов разбиения фигуры на более простые формы — использование треугольников. Если внимательно рассмотреть неправильную фигуру, часто можно найти в ней треугольники, для которых уже известны формулы для расчета площади. Путем выделения и вычисления площади каждого треугольника, можно затем сложить их площади, получив общую площадь фигуры.
Разбиение на прямоугольники
Еще одним методом разбиения фигуры на более простые формы является разбиение на прямоугольники. Площадь прямоугольника можно легко вычислить, умножив длину на ширину. Путем разбиения фигуры на несколько прямоугольников и последующего сложения их площадей, можно получить общую площадь фигуры.
Разбейте фигуру на более простые формы
При работе с фигурами неправильной формы, часто нам требуется вычислить их площадь. Однако, вместо того чтобы пытаться найти точную формулу для каждой фигуры, можно использовать метод разбиения на более простые формы.
Этот метод позволяет разделить фигуру на несколько более простых форм, таких как прямоугольники, треугольники или круги. Затем можно вычислить площадь каждой из этих форм и сложить их вместе, чтобы получить общую площадь фигуры.
| Форма | Формула для вычисления площади |
|---|---|
| Прямоугольник | Ширина * Высота |
| Треугольник | (Основание * Высота) / 2 |
| Круг | Пи * Радиус 2 |
После того, как вы вычислите площади каждой из простых форм, сложите их вместе, чтобы получить общую площадь фигуры неправильной формы. Этот метод позволяет нам упростить вычисление площади и решить задачу даже для сложных фигур.
Изучите структуру и свойства сложных геометрических фигур
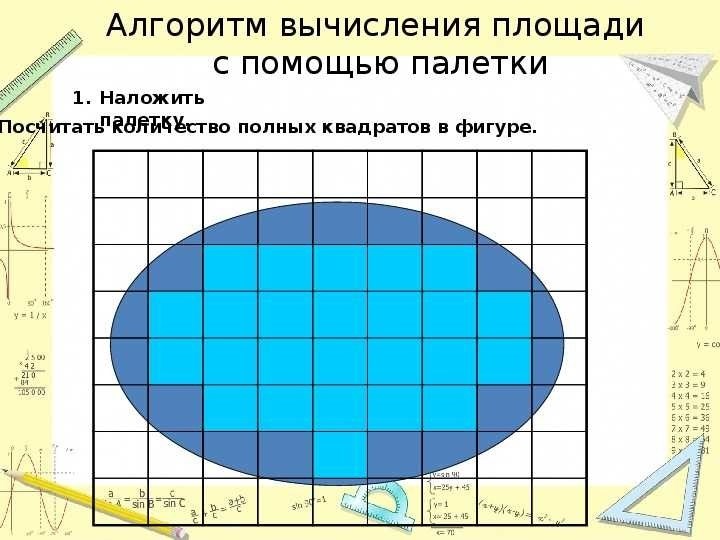
В этом разделе мы рассмотрим способы изучения формы сложных геометрических фигур, которые не подчиняются обычным правилам и определениям. Мы предлагаем вам применить аналитический подход к изучению этих фигур, чтобы лучше понять их структуру и свойства. Вместо простого подсчета площади мы сосредоточимся на исследовании формы и соотношений между различными частями фигуры.
Прежде чем приступить к изучению сложных фигур, важно разбить их на более простые формы. Это позволит нам анализировать их компоненты отдельно и затем объединять полученные знания, чтобы полностью понять структуру всей фигуры. Мы рассмотрим несколько примеров разбиения фигур на более простые составляющие и обсудим, как эти составляющие взаимодействуют друг с другом.
Одним из ключевых аспектов изучения сложных геометрических фигур является определение их уникальных свойств и характеристик. Мы обратимся к задаче определения и классификации сложных форм и рассмотрим, какие факторы могут влиять на их свойства. Например, мы можем исследовать, как изменение размера, пропорций или углов влияет на форму и структуру фигуры.
В конечном итоге, изучение сложных геометрических фигур поможет нам получить глубокое понимание их структуры и свойств. Мы узнаем, как взаимодействуют различные элементы фигуры, какие закономерности и соотношения можно найти, а также как эти знания могут быть применены в практических ситуациях. В следующих разделах мы подробно разберем различные аспекты изучения сложных геометрических фигур и предоставим вам полезные инструменты и методы для работы с ними.
Изучите конструкцию геометрической фигуры
В этом разделе рассмотрим, как изучить конструкцию неправильной фигуры и определить ее особенности. Для этого мы разобъем фигуру на более простые формы и изучим каждую из них подробно. Такой подход позволяет нам получить полное представление о структуре фигуры и определить ее площадь.
При анализе фигуры нам помогут ключевые идеи из математического учебника Big Ideas Math. Они позволяют нам использовать определенные методы и подходы для решения задач по геометрии. Также воспользуемся ответами из Eureka Math Answer Key для проверки наших расчетов и уточнения результатов.
Перед тем, как приступить к подробному изучению формы фигуры, важно осознать основные понятия, связанные с неправильными фигурами. В этом нам поможет определение Irregular Shapes, которое описывает такие фигуры и указывает на их специфические черты.
Далее мы разобьем фигуру на более простые формы, такие как прямоугольники, треугольники и т.д. Это позволит нам лучше понять структуру фигуры и произвести необходимые расчеты. Мы воспользуемся методами и алгоритмами из математического учебника, которые помогут нам определить площадь каждой из простых форм и суммировать их, чтобы получить общую площадь всей фигуры.
Итак, изучение формы неправильной геометрической фигуры требует разбиения ее на более простые формы и анализа каждой из них. Наша методика основана на ключевых идеях из математических учебников и проверена с помощью Eureka Math Answer Key. Такой подход дает нам возможность точно определить площадь фигуры и получить полное представление о ее конструкции.